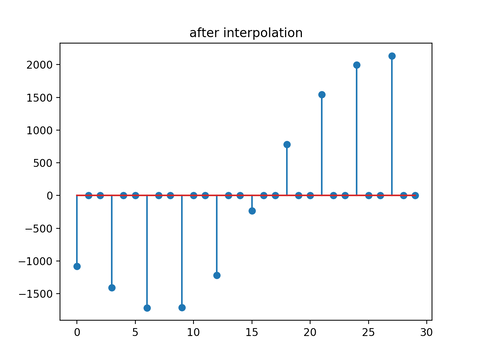
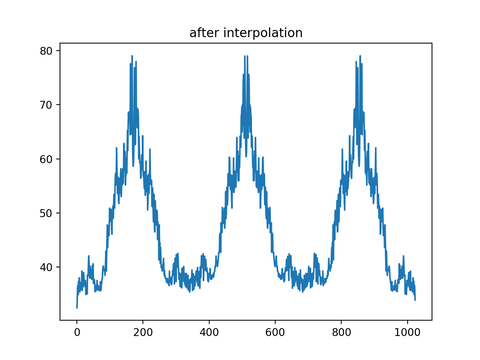
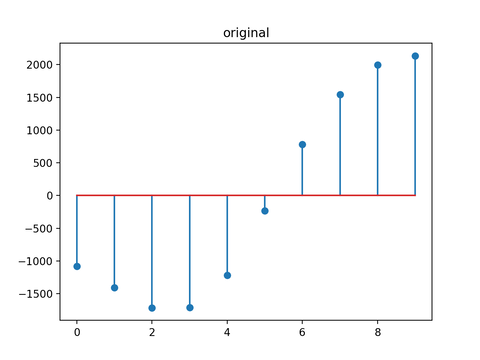
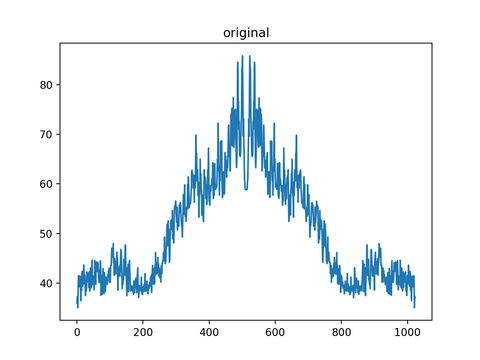
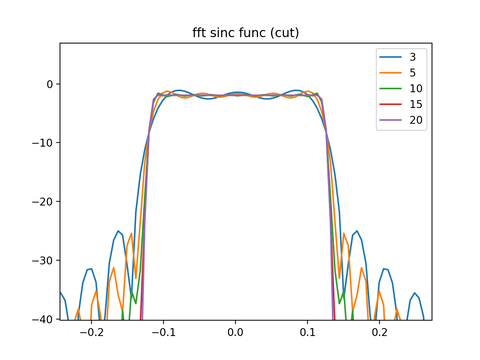
ごくごく簡単なスクリプトで以前にも実行していたのに、なぜかsegmentation fault 11が発生している。
デバッグしたところ、plot.show()で発生している。
何かしたかな?と考えたところ、そういえば、OSをBIg Surにあげたと。
検索してみると、同様の問題は発生していて、matplotlibをアンインストールして再度インストールしろと。
で、ターミナルから
conda uninstall matplotlib
でアンインストールして
conda install matplotlib
でインストールした。
これで動くかと思ったら今度は
no module named scipy
とでてしまう。
conda install scipy
でインストールしたら、とりあえずスクリプトは実行できるようになった。